
Babilonia argilo tablojdo YBC 7289 (c. 1800-1600 aK) kun komentarioj. La proksimuma kalkulado de la kvadrata radiko de 2 estas kvar sexagesimales figuroj, kiuj estas ĉirkaŭ ses dekuma figuroj. 1 + 24/60 + 51/60 2 + 10/60 3 = 1,41421296 ... [1]
Cifereca analitiko estas la studo de
algoritmoj kiuj uzas nombrajn
proksimumajn kalkuladojn (kontraste al ĝeneralaj
simbolaj manipuladoj) por la problemoj de
matematika analizo (kiel distingita de
diskreta matematiko).
Unu el la plej fruaj matematikaj skriboj estas babilonia briketo el la
Yale Kolekto de Babilonoj (YBC 7289), kiu donas sesemaj nombraj
proksimuma kalkulado de

. La longo de la diagonalo en unuobla kvadrato.
Povante komputi la flankojn de triangulo (kaj do, povante komputi
kvadratajn radikojn) estas ege grava, ekzemple, en lignaĵejo kaj konstruo.
[2]
Cifereca analitiko daŭrigas tiun longan tradicion de praktikaj matematikaj kalkuloj. Same kiel la babilonaj proksimumaj kalkuladoj de

. Moderna cifereca analitiko ne serĉas ĝustajn respondojn, ĉar ĝustaj respondoj estas ofte neebla atingi praktike. Anstataŭe, multa da cifereca analitiko estas koncernita kun akiri proksimumajn solvojn subtenante raciaj baroj sur eraroj.
Cifereca analitiko nature trovas aplikojn en ĉiuj kampoj de inĝenierio
kaj la fizikaj sciencoj, sed en la 21a jarcento, la vivaj sciencoj kaj eĉ
la artoj adoptis elementojn de sciencaj kalkuladoj.
Ordinaraj diferencialaj ekvacioj aperas en la
movado de ĉielaj korpoj (planedoj, steloj kaj galaksioj) ;
cifereca lineara algebro estas grava por analizi datumojn;
stokastaj diferencialaj ekvacioj kaj
Markovaj ĉenoj estas esence simulo kiu habitas ĉelojn por medicino kaj biologio.
Antaŭ la alveno de modernaj komputilaj nombraj metodoj ofte dependis de manan
interpolon en grandaj presitaj tabloj. Ekde la mezo 20a jarcento, komputiloj kalkuli la necesajn funkciojn anstataŭe. Tiuj samaj interpolaj formuloj tamen daŭre esti uzita kiel parto de la programaraj
algoritmoj por solvi
diferencialajn ekvaciojn.
Ĝenerala enkonduko
La ĝenerala celo de la kampo de cifereca analitiko estas la dezajno kaj
analizo de teknikoj por doni proksimuman sed precizaj solvaĵoj al
malmolaj problemoj, la diversajn kiu estas sugestita de la sekva.
- Altnivelaj nombraj metodoj estas esenca fari nombran veteran antaŭdiron farebla.
- Komputante la trajektorio de kosmoŝipo postulas la precizajn ciferecajn solvaĵojn de sistemo de ordinaraj diferencialaj ekvacioj.
- Aŭto-entreprenoj povas plibonigi la akcidentan sekurecon de siaj veturiloj uzante komputilan simulecoj de aŭto-eraroj. Tia simuleco esence konsistas solvi partajn diferencialajn ekvaciojn ciferece.
- Hedge funds
(privataj investadaj fondusoj) uzas ilojn de ĉiuj kampoj de cifereca
analitiko provi kalkuli la valoron de akcioj kaj derivitaj pli precize
ol aliaj merkataj partoprenantoj.
- Airlines uzas kompleksajn optimumigajn algoritmojn por decidi biletajn prezojn, aviadilo kaj ŝipanaj atribuoj kaj brulaĵaj bezonoj. Historie, tiaj algoritmoj estis disvolvitaj en la solapanda kampo de operaciesploro.
- Asekuroj uzas nombrajn programojn por aktuala analitiko.
La resto de ĉi tiu sekcio skizas kelkajn gravajn temojn de cifereca analitiko.
Historio
La kampo de cifereca analitiko estas antaŭa la invento de modernaj komputiloj de multaj jarcentoj.
Lineara interpolo estis jam uzata pli ol 2000 jaroj.
Multaj grandaj matematikistoj de la pasinteco estis okupata de cifereca
analitiko, kiel estas evidenta da la nomoj de gravaj algoritmoj kiel
maniero de
Neŭton,
interpola polinomo de Lagrange,
elimino de
Gaŭsa, aŭ
metodo de
Eŭler.
Havigi kalkuladojn mane, grandaj libroj estis produktitaj kun formuloj
kaj tabloj de datumoj kiel interpolaj punktoj kaj funkciaj koeficientoj.
Uzante ĉi tiuj tabloj, ofte kalkulata al 16 dekumaj lokoj aŭ pli por iuj
funkcioj, oni povus serĉi valorojn plugi en la formuloj donata kaj
atingas tre bonaj nombraj korinklinoj de iuj funkcioj. La kanona laboro en la kampo estas la
NIST-publikigo redaktita de
Abramowitz kaj Stegun, 1000-plus paĝa libro de tre granda nombro de komunaj uzitaj formuloj kaj funkcioj kaj iliaj valoroj en multaj punktoj.
La funkciaj valoroj ne plu estas tre utila kiam komputilo estas
disponebla, sed la granda listo de formuloj povas ankoraŭ esti tre
oportuna.
La
mekanika kalkulilo disvolvis ankaŭ kiel ilo por mane kalkuli.
Tiuj kalkuliloj evoluis elektronikajn komputilojn en la jaroj 1940, kaj
estis tiam trovita ke tiuj komputiloj estis ankaŭ utila por administraj
celoj.
Sed la invento de la komputilo ankaŭ influis la kampon de cifereca
analitiko, ekde nun pli kaj pli komplikaj kalkuloj povus fari.
Rektaj kaj ripetaj manieroj
Rekta vs ripetaj manieroj
Pripensu la problemon de solvanta
- 3 x 3 + 4 = 28
por la nekonata kvanto x.
Rekta metodo
| 3 x 3 + 4 = 28. |
| Subtrahi 4 | 3 x 3 = 24. |
| Dividi per 3 | x 3 = 8. |
| Prenu kubaj radikoj | x = 2. |
Por la ripeta maniero, apliku la bisection metodo al f (x) = 3 x 3 - 24. La komenca valoroj estas a = 0, b = 3, f (a) = -24, f (b) = 57.
Ripeta maniero
| oni | b | meze | f (meze) |
|---|
| 0 | 3 | 1.5 | -13,875 |
| 1.5 | 3 | 2.25 | 10,17 ... |
| 1.5 | 2.25 | 1,875 | -4,22 ... |
| 1,875 | 2.25 | 2,0625 | 2,32 ... |
Ni konkludas el tiu tablo ke la solvo estas inter 1,875 kaj 2,0625. La algoritmo povas redoni ajna nombro en tiu gamo kun eraro malpli ol 0,2.
diskretiga kaj cifereca integralado
En du minutoj raso, ni mezuris la rapidon de la aŭto en tri momentoj kaj gravuritaj ilin en la sekva tabelo.
| Tempo | 0:20 | 1:00 | 1:40 |
|---|
| km / h | 140 | 150 | 180 |
|---|
Al diskretiga estus diri ke la rapido de la aŭto estis konstanta de 0:00 ĝis 0:40, tiam de 0:40 ĝis 1:20 kaj fine de 1:20 ĝis 2:00. Ekzemple, la tuta distanco vojaĝis en la unuaj 40 minutoj estas proksimume (2/3h × 140 km / h) = 93.3 km. Ĉi tio permesos al ni taksi la tuta distanco vojaĝis kiel 93.3 km + 100 km + 120 km = 313,3 km, kiu estas ekzemplo de cifereca integralado (vidu sube) uzante Rimana sumo , ĉar movo estas la integralo de vektora rapideco.
Malsana afektita problemo: Prenu la funkcio f (x) = 1 / (x - 1). Notu ke f (1.1) = 10 kaj f (1.001) = 1000: ŝanĝo en x de malpli ol 0,1 igas ŝanĝon en f (x) de preskaŭ 1000. Taksante f (x) proksime x = 1 estas malsana klimatizita problemo.
Bone afektita problemo: Per kontrasto, la funkcio  estas kontinua kaj tiel taksi estas bone afektita, almenaŭ por x estas ne proksime al nulo. estas kontinua kaj tiel taksi estas bone afektita, almenaŭ por x estas ne proksime al nulo. |
Rektaj metodoj komputas la solvon al problemo en finia nombro de paŝoj. Tiuj metodoj donus la precizan respondon se ili estis ludataj en
malfinia precizeca aritmetiko. Ekzemploj inkluzivas
elimino Gaŭs, la faktoriga maniero de
QR por solvi
sistemojn de linearaj ekvacioj kaj la
simpleca maniero de
lineara programado. Praktike,
finiaj precizecoj estas uzata kaj la rezulto estas proksimuma kalkulado de la vera solvo (supozante
stabileco).
Kontraste al rektaj metodoj,
ripetaj manieroj ne atendis por nuligi en nombro de paŝoj. Ekde komenca konjekto, ripetaj manieroj formas sukcesajn proksimumajn kalkuladojn ke
konverĝas al la ĝusta solvo nur en la limo. La
konverĝa testo specifas por decidi kiam sufiĉe preciza solvo (espereble) estis trovita. Eĉ uzante malfinia precizeca aritmetiko tiuj metodoj ne atingas la solvon ene finia nombro de paŝoj (ĝenerale). Ekzemploj inkluzivas
Neŭtona maniero, la
bisekcia metodo, kaj
Jakobia ripeto. En komputa matrica algebro, ripetaj manieroj estas ĝenerale bezonata por grandaj problemoj.
Ripetaj manieroj estas pli komuna ol rektaj metodoj en cifereca analitiko. Iuj metodoj estas rekta principe sed kutime uzata kvazaü ili ne estis, ekzemple,
GMRES kaj la
konjugita gradienta maniero.
Por ĉi tiuj metodoj la kvanto da paŝoj necesas akiri la ĝustan
solvon tiel granda ke alproksimiĝo estas akceptita en la sama
maniero kiel pro ripeta metodo.
diskretigo
Plue, kontinuaj problemoj devas iam esti anstataŭigita per diskreta
problemo kies solvaĵo estas konata aproksimante tiu de la kontinua
problemo; tiu procezo estas nomata
diskretigi. Ekzemple, la solvaĵo de
diferenciala ekvacio estas funkcio.
Ĉi tiu funkcio devas esti prezentita per finia kvanto da datumoj,
ekzemple per ĝia valoro je finia nombro de punktoj je ĝia domajno,
kvankam ĉi domajno estas kontinuaĵo.
Generacio kaj disvastigo de eraroj
La studo de eraroj formas gravan parton de cifereca analitiko. Estas pluraj manieroj en kiuj eraro povas esti enkondukita en la solvo de la problemo.
Rondiga Eraroj
Rondigo eraroj ekestas ĉar estas neeble por reprezenti tutajn
reelajn nombrojn ĝuste sur maŝino kun finia memoro (kiu estas kio ĉiuj praktikaj
ciferecaj komputiloj estas).
Tranĉa kaj diskretiga eraro
Tranĉaj
eraroj faras kiam ripeta maniero estas finita aŭ matematika proceduro
estas proksimuma, kaj la aproksima solvaĵo diferencas la ĝustan
solvon. Simile, diskretigi konkludas
diskretigan eraron ĉar la solvo de la diskreta problemo ne koincidas kun la solvo de la kontinua problemo. Ekzemple, en la ripeto en la flanka kolumno komputi la solvon de
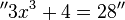
, Post 10 aŭ tiel iteracioj, ni konkludas, ke la radiko estas proksimume 1.99 (ekzemple). Ni do havas tranĉan eraron de 0.01.
Iam eraro estas generita, ĝi ĝenerale propagas tra la ŝtono. Ekzemple, ni jam rimarkis, ke la operacio + sur kalkulilo (aŭ komputilo) estas ne-perfekta. Sekvas, ke oni kalkulas de la tipon a + b + c + d + e estas eĉ pli ne-perfekta.
Kion tio signifas kiam oni diras ke la tranĉa eraro estas kreita kiam ni proksimumas matematikan proceduron? Ni scias ke por integri funkcion ĝuste postulas por trovi la sumon de senfinaj trapezoidoj. Sed numere oni povas trovi la sumon de nur finia trapezoidoj, kaj sekve la proksimuma kalkulado de la matematika proceduro.
Simile, por diferenci funkcion, la diferenciala elemento alproksimiĝas
al nulo sed numere ni povas nur elekti finian valoron de la diferenciala
elemento.
Cifereca stabileco kaj bone afektitaj problemoj
Cifereca stabileco estas grava nocio en cifereca analitiko. Algoritmo estas nomita
nombre stabila se eraro, kia ajn ĝia kaŭzas
, ne kreskas esti multe pli granda dum la ŝtono. Tio okazas, se la problemo estas
bonkondiĉa, signifante ke la solvaj
ŝanĝoj de nur malgranda kvanto, se la problemaj datumoj ŝanĝiĝis per malgranda kvanto. Kontraŭe, se problemo estas
malsana klimatizita, tiam ajna malgranda eraro en la datumoj kreskos esti granda eraro.
Tiel la originala problemo kaj la algoritmo uzita por solvi tiun problemon eblas esti
bonkondiĉa kaj/aŭ
malsane klimatizita, kaj ajna kombino estas ebla.
Do algoritmo kiu solvas bonkondiĉa problemo povas esti ĉu ciferece stabila aŭ ciferece malstabila. Arto de cifereca analitiko estas trovi stabilan algoritmon por solvi bone afektita matematika problemo. Ekzemple, komputante la kvadrata radiko de 2 (kiu estas krude 1.41421) estas bone-afektita problemo. Multaj algoritmoj solvas ĉi tiun problemon startante kun komenca alproksimiĝo
x1 ĝis

, Ekzemple
x1 = 1.4, kaj poste kalkuli plibonigita diveno
x2, x3, ktp. Unu tia metodo estas la fama
babilona maniero, kiu estas donita per
xk+1 =
xk / 2 + 1/
xk. Alia ripeto
, kiu nomos X-Metodo, estas donita per
x k +1 =
(x k 2 -2)
2 +
x k. [3] Ni kalkulis kelkajn iteraciones de ĉiu skemon en tabelo suban formularon, kun komenca divenas
x 1 = 1,4 kaj
x 1 = 1,42.
| Babilonia | Babilonia | X-Metodo | X-Metodo |
|---|
| x1 = 1,4 | x1 = 1,42 | x1 = 1,4 | x1 = 1,42 |
| x2 = 1.4142857 ... | x2 = 1.41422535 ... | x2 = 1.4016 | x2 = 1.42026896 |
| x3 = 1.414213564 ... | x3 = 1.41421356242 ... | x3 = 1.4028614 ... | x3 = 1.42056 ... |
|
| ... | ... |
|
| x 1000000 = 1,41421 ... | x 28 = 7280.2284 ... |
Observi ke la babilona maniero konverĝas rapida sendepende de la
komenca guess, dum Metodo X konverĝas ekstreme malrapide kun komenca
guess 1.4 kaj diverge por komenca guess 1,42. Sekve, la babilona maniero estas ciferece stabila, dum Metodo X estas ciferece malstabila.
- Cifereca stabileco
estas tuŝita de la nombro de la signifaj ciferoj la maŝino daŭre, se ni
uzas maŝinon kiu tenas en la unuaj kvar glitpunkta, glitkoma ciferoj,
bona ekzemplo de perdo de graveco estas donita per ĉi tiuj du
ekvivalentaj funkcioj
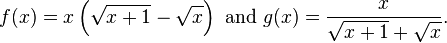
- Se ni komparas la rezultojn de

- kaj

- per rigardado al la du supre rezultojn, ni rimarkas ke perdo de signifo kiu estas ankaŭ nomata subtraha Cancelation
havas grandegan efikon sur la rezultoj, kvankam ambaŭ funkcioj estas
ekvivalentaj, por montri ke ili samvaloras simple ni devas starti per f(x) kaj fine kun g(x), kaj tiel
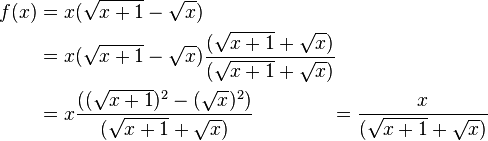
- La vera valoro por la rezulto estas 11.174755 ..., kiu estas ĝuste g(500) = 11.1748 post rondigas la rezulto al 4 dekumaj ciferoj.
- Nun imagu ke multaj terminoj kiel tiuj funkcioj estas uzataj en la
programo; la eraro pliigos kiel unu procedas en la programo, krom se oni
uzas la taŭgan formulon de la du funkcioj ĉiufoje unu taksas ĉu f (x), aŭ g (x ); la elekto dependas de la pareco de x.
- La ekzemplo estas prenita de Mathew; Nombraj metodojn uzante Matlab, 3a eld.
Areoj de studo
La kampo de cifereca analitiko estas dividita en malsamaj disciplinoj laŭ la problemo, kiun oni devas solvi.
Komputado de valoroj de funkcioj
Interpola: Ni observis la temperaturo al varias de 20 gradoj Celsius je 1:00 ĝis 14 gradoj je 3:00. Lineara interpolo de ĉi datumoj devus konkludi, ke ĝi havis 17 gradoj je 2:00 kaj 18,5 gradoj je 1:30 ptm.
Extrapolación: Se la malneta interna produkto
de lando estis kreskanta mezumo de 5% por jaro kaj estis 100 miliardoj
da dolaroj pasintjare, ni povus extrapolar ke estos 105 miliardoj da
dolaroj ĉi-jare.
Malprogreso: En lineara malprogreso, donita n punktoj, ni komputi linion kiu pasas kiel fermi kiel eblas tiuj n punktoj.
Optimumigo: Diru vi vendas limonadon ĉe limonado piedestalon
, kaj rimarkas ke en $ 1, vi povos vendi 197 glasojn da limonado tage,
kaj ke por ĉiu kresko de $ 0,01, vi vendos unu glaso da limonado malpli
tage. Se
vi povus ŝarĝi $ 1,485, vi maksimumigi vian profito, sed pro la limigo
de devi ŝarĝi tuta cendo kvanto, enspezante $ 1.49 po glason estos
liveri la maksimuma revenuo di $ 220,52 por tago.
Diferenciala ekvacio: Se vi starigis 100 fanoj blovi aero de unu fino de la salono al la alia kaj tiam vi faligis plumo al la vento, kio okazas? La plumo sekvos la aero fluoj, kiu povas esti tre kompleksa.
Unu proksimuma kalkulado estas por mezuri la rapidon je kiu la aero
blovas proksime de la plumo ĉiu dua, kaj antaŭenigi la simulitaj plumo
kvazaŭ movis en rekta linio je tiu sama rapido por dua, antaŭ mezurante
la rapido de la vento denove. Tiu nomiĝas la Eŭlera maniero por solvanta ordinara diferenciala ekvacio. |
Unu el la plej simplaj problemoj estas la pritakso de funkcio je donita punkto. La plej simpla alproksimiĝo, de nur ŝtopanta en la nombro en la formulo estas kelkfoje ne tre efika. Por polinomoj, pli bonan alproksimiĝon uzas la
skemo de
Horner, pro tio reduktas la necesan numeron de multiplikoj kaj aldonoj. Ĝenerale, estas grave por estimi kaj kontroli
rondigo eraroj kiuj rezultas el la uzo de
flosanta punkto aritmetiko.
Interpolo, ekstrapolo kaj malprogreso
Interpolo
solvas la sekvan problemon: donita la valoro de iu nekonata funkcio je
nombro de punktoj, kio valoro ne tiu funkcio havas en iu alia punkto
inter la donita punktoj?
Ekstrapolo
estas tre simila al interpolado, krom ke nun ni volas trovi la valoron
de la nekonata funkcio je punkto, kiu estas ekster la donitaj punktoj.
Malprogreso estas ankaŭ simila, sed enkalkulas ke la datumoj estas malpreciza.
Donita iuj punktoj, kaj mezuro de la valoro de iu funkcio je ĉi tiuj
punktoj (kun eraro), ni volis determini la nekonatan funkcion. La
minimumaj kvadratoj -metodo estas unu popularaj manieroj atingas tion.
Solvantaj ekvacioj kaj
ekvaciaj sistemoj
Alia fundamenta problemo estas komputanta la solvo de iu donita ekvacio. Du kazoj estas kutime distingas, depende de ĉu la ekvacio estas lineara aŭ ne. Ekzemple, la ekvacio

estas lineara tempo
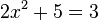
ne estas.
Tre penado estis metita en la disvolviĝo de metodoj por solvi
sistemojn de linearaj ekvacioj . Norma rektaj metodoj, tio estas, metodoj kiuj uzas iujn
matrico malkomponaĵo estas
elimino de Gaŭsa,
LU malkomponaĵo ,
malkomponaĵo de
Cholesky por
simetria (aŭ
hermita) kaj
pozitiva-definitiva matrico, kaj
QR malkomponaĵo por ne-kvadrataj matricoj.
Ripetaj manieroj kiel la
metodo de
J ,
metodo de Gaŭso-Seidel,
pluaj super-malstreĉiĝo kaj
konjugita gradienta maniero estas kutime preferis grandajn sistemojn. Ĝenerala ripetaj manieroj povas disvolvi uzante
matrica disiĝo.
Radiko-trovaj algoritmoj
estas uzataj por solvi nelinearaj ekvacioj (ili estas tiel nomata ĉar
radiko de funkcio estas argumento por kiu la funkcio rendimenta nulo). Se la funkcio estas
diferencialebla kaj la derivaĵo estas konata, tiam
metodo de
Neŭton estas populara elekto.
Linearization estas alia tekniko por solvi nelinearajn ekvaciojn.
Solvanta ajgeno aŭ singularaj valoraj problemoj
Pluraj gravaj problemoj povas esti verkitaj en terminoj de
ajgeno malkomponaĵoj aŭ
singulara valoro malkomponaĵoj . Ekzemple, la
spektra bilda kunprema algoritmo
[4] estas bazita en la singulara valora malkomponaĵo. La responda ilo en statistiko estas nomita
ĉefa komponanta analitiko .
Optimumigo
Optimumigo problemoj peti la punkto je kiu donita funkcio estas maksimumigita (aŭ minimumigita). Ofte, la punkto ankaŭ devas kontentigi iujn
limigojn .
La kampo de optimumigo estas plui fendi en pluraj subcampos, depende de la formo de la objektiva funkcio kaj la limigo. Ekzemple,
lineara programado traktas la kazon kiu ambaŭ la objektiva funkcio kaj la limigoj estas lineara. Fama metodo en lineara programado estas la
simpleca maniero.
La metodo de
multiplikantoj de Lagrange povas uzi por redukti optimumigo problemojn kun limigoj al unconstrained optimumigo problemojn.
Taksante integraloj
Cifereca integralado, en iuj kazoj ankaŭ sciata kiel cifereca
kvadraturo , petas la valoro de difinita
integralo . Populara metodoj uzi unu el la
formuloj de Neŭtono-Cotes (kiel la mezpunkton regulo aŭ
Simpson regulo ) aŭ
kvadraturo de
Gaŭsa.
Tiuj metodoj fidi al "dividi kaj venki" strategio, per integralo sur
relative granda aro estas rompita malsupren en integraloj sur malgrandaj
aroj. En pli altaj dimensioj, kie ĉi tiuj metodoj fariĝis prohibitivamente peniga en terminoj de komputa peno, oni povas uzi
Montekarlo aŭ
kvazaŭ-Montekarlo metodoj (vidu
integriĝon de
Montekarlo ), aŭ, en modeste grandaj dimensioj, la metodo de
maldensa kradoj.
Diferencialaj ekvacioj
Cifereca analitiko estas ankaŭ pri komputado (en proksimuma maniero). La solvo de
diferencialaj ekvacioj, ambaŭ ordinaraj diferencialaj ekvacioj kaj
partaj diferencialaj ekvacioj.
Partaj diferencialaj ekvacioj estas solvitaj per unua discretizing la ekvacio, alportante ĝin en finidimensia subspaco. Ĉi tiu povas esti farita de
finia era maniero , oni
finia diferenco metodo, aŭ (speciale en inĝenierado) estas
finia volumo metodo . La teoria pravigo de ĉi tiuj metodoj ofte engaĝas teoremoj de
funkcionala analitiko. Ĉi tio reduktas la problemon al la solvo de algebra ekvacio.
Programoj
Ekde la malfrua dudeka jarcento, plej algoritmoj realigitajn en vario de programlingvoj. La
Netlib dosieraro enhavas diversajn kolektojn de programaro rutinoj por cifereca problemoj, ĉefe en
Fortran kaj
C . Komercaj produktoj implementando multaj malsamaj nombraj algoritmoj inkluzivi la
IMSL kaj
Nag bibliotekoj; libera alternativo estas la
GNU Scienca Biblioteko .
Estas pluraj popularaj nombraj komputado aplikoj kiel
_MATLAB_ ,
S-PLUS ,
LabVIEW , kaj
IDL tiel kiel senpaga kaj malfermita kodo alternativoj kiel
FreeMat ,
Scilab ,
GNU Octave (simila al Matlab),
IT + + (C + + biblioteko),
R ( simila al S-PLUS) kaj iuj variantoj de
Python .
Agado varias vaste: dum vektoro kaj matrico operacioj estas kutime
rapida, skalaro maŝojn povas varii en rapido de pli ol ordo de grando.
[5] [6]
Multaj
komputilo algebro sistemoj kiel
Mathematica ankaŭ profitus el la disponebleco de
arbitraj precizeco aritmetiko kiu povas havigi pli precizaj rezultoj.
Ankaŭ, ĉiu
folio programaro povas esti uzata por solvi simplajn problemojn rilate al cifereca analitiko.

 . La longo de la diagonalo en unuobla kvadrato.
Povante komputi la flankojn de triangulo (kaj do, povante komputi
kvadratajn radikojn) estas ege grava, ekzemple, en lignaĵejo kaj konstruo.
. La longo de la diagonalo en unuobla kvadrato.
Povante komputi la flankojn de triangulo (kaj do, povante komputi
kvadratajn radikojn) estas ege grava, ekzemple, en lignaĵejo kaj konstruo.
 estas kontinua kaj tiel taksi estas bone afektita, almenaŭ por x estas ne proksime al nulo.
estas kontinua kaj tiel taksi estas bone afektita, almenaŭ por x estas ne proksime al nulo.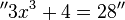 , Post 10 aŭ tiel iteracioj, ni konkludas, ke la radiko estas proksimume 1.99 (ekzemple). Ni do havas tranĉan eraron de 0.01.
, Post 10 aŭ tiel iteracioj, ni konkludas, ke la radiko estas proksimume 1.99 (ekzemple). Ni do havas tranĉan eraron de 0.01. 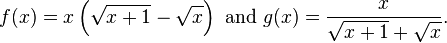


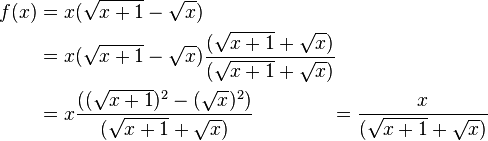



 estas lineara tempo
estas lineara tempo 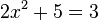 ne estas.
ne estas.